Drawdown y Esperanza matemática

DD y EM

¿En qué se basa?

Existen distintas formas de medir el posible Drawdown (máxima pérdida) en base a distintos parámetros. Una de las formas que uso simplificando de forma genérica y válido para cualquier estrategia es la que se mide en base a la esperanza matemática(EM). 

El razonamiento es el siguiente: al final una curva de equity recorre un camino estocástico de pérdidas y ganancias aleatorias(probabilidad) con una estrategia de esperanza matemática cero el camino que recorre es completamente aleatorio y hay las mismas probabilidades de que suba que de que baje. Conforme la EM aumenta se va a ganar y perder como siempre, pero no de la misma forma por cada operación que se realice se aporta un valor añadido a la curva del equity que hace que no sea igual de probable que caiga que de que suba. Cuanto mayor es la EM más alcista es la curva de equity y menos duradero y profundo de media serán las caídas del equity, es decir, el Drawdown (DD). 

Resulta que cuanto mayor sea la EM más pequeño será el DD máximo probable que tendrá la estrategia, esto tiene su lógica porque la EM es la relación entre la fiabilidad de la estrategia (porcentaje de acierto respecto de fallo) y el retorno y pérdida media por operación. Por ejemplo, cuanto mayor sea la fiabilidad de la estrategia a una misma perdida y ganancia media menos probable se va  haciendo obtener una racha perdedora hasta el punto de que al 100% de acierto no se tiene DD alguno posible (caso utópico). 

Pues conociendo la EM y el riesgo medio por operación (uso el 1%) se puede calcular la probabilidad de máximo DD para cualquier estrategia de forma aproximada. En la práctica es sumamente más complejo, porque para acercarnos bien necesitaríamos el EM exacto y el riesgo medio por operación exacto, cosa que es difícil. Esto se debe a que, por ejemplo, en los datos de darwinex te dan los pips medios por operación, pero cada activo tiene un valor distinto para cada pip ya que no es lo mismo un eurusd a 1,1000 que un gbpaud a 1,8000 menos aun los pips del oro que ponderan mucho más. De manera que te puedes encontrar estrategias que pierden con EM positiva y la inversa. Para estrategias que tengan una gran muestra y operando siempre en mismos activos este ruido disminuye aunque sigue ahí, pues un mismo activo cambia de precio con el tiempo y en consecuencia el valor del pip.

Aplicado a Darwinex

Esto lo he aplicado a los datos que tengo de los darwins para calcular en excel los probable DD de algunos darwins en los que invierto. En la pestaña activos y horarios se puede sacar el porcentaje de acierto de la estrategia, la pérdida media y la ganancia media para sacar la EM, el riesgo medio por operación del 1% va bien de forma aproximada para el VaR del 10% que usan los darwins aunque el valor real es otro y no tengo forma de saberlo a día de hoy.

Modo de calcularlo

En excel hago una simulación con los datos recogidos para que me arroje aleatoriamente 3000 operaciones teniendo en cuenta la EM dada por los datos. Al tener EM positiva la cuerva será alcista la mayoría de las veces. Para sacar una distribución aproximada de posibles máximos DD para 3000 operaciones con una macro hago que se repita el proceso unas 1000 iteraciones (pueden ser más o menos según le pidas) y ya ahí te saldrá una campana de gauss que conforme tenga la EM mayor se desplazará más hacia la izquierda como es de esperar. Procederé a calcularlo con mi darwin de mayor muestra, UYZ.

UYZ

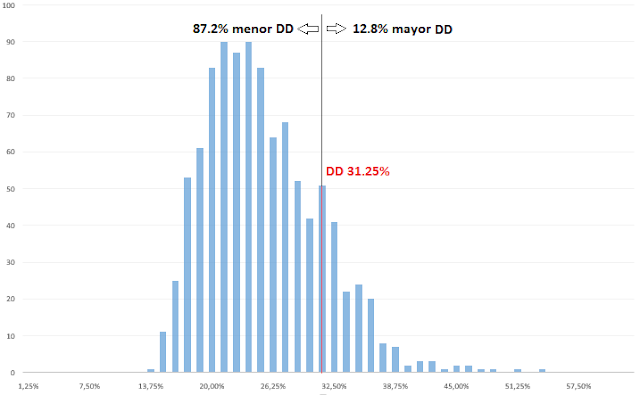
He procedido al cálculo del DD probable para el darwin UYZ después 1000 simulaciones de 3000 operaciones y hay una probabilidad del 87.2% con la actual EM de que el DD se mantenga por debajo del 31.25%. Pudiendo ser mayor hasta en un 12.8% de ocasiones. Adjunto imagen de la distribución. Para contextualizar el darwin en 5 años ha hecho 5000 operaciones y la simulación equivaldría a 600 años de trading con la EM actual.

Hay que tener claro que la distribución depende de la esperanza matemática y el riesgo (en el caso del darwin al ser constante solo de la EM) si la esperanza cambiara el DD lo haría en consonancia. Mejorar la EM disminuiría el DD y lo contrario, por lo que habría que ir contextualizando cada cierto tiempo para adaptar el DD máximo probable actual.

Conclusión

Relacionar la EM y el DD puede dar un riesgo máximo aproximado que esperar, pero la fiabilidad del resultado dependerá de la calidad y exactitud de los datos. En mi caso uso también el simulador de montecarlo, pero al variar el riesgo de la estrategia con el tiempo sería más interesante hacerlo con el darwin que tiene VaR constante y para eso el método de la EM me parece más interesante, pero se necesitaría saber el riesgo exacto e igualar la perdida y ganancia media entre activos para que tuvieran el mismo valor.

Disclaimer: Los comentarios recogidos en este documento no representan asesoramiento financiero alguno y su uso es meramente informativo y educativo.

SK Trading